Koch曲线的动态化
更新日期:
上周在Matrix67的博客里看到了一个有点意思的博文《7 个分形图形的动画演示》,而Matrix67并没有给出他的源代码,外加我曾经写过Koch曲线的代码,只差一个动态化的过程,所以就决定补一个代码。

首先不考虑动态部分,只考虑怎么获得我们画图需要的点的具体坐标位置。在这里,我用的方法是一种特别简单明了的方法,其思路可以用下面这个图表示,用语言来描述的话,就是已知1个线段的始末点坐标,先寻找2个三等分点,然后将第2个三等分点围绕第1个三等分点逆时针旋转60度,即可得到5个点,其中前4个点保留(因为最后一个点,是下一个线段的第一个点,无需重复保留)。这个是我自己的思路,看上去代码挺多的,但是胜在直观形象。关于Koch曲线的其他数据生成方式,可以参考这里。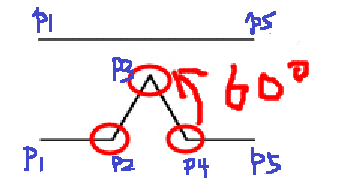
其MMA实现为:
Clear["Global`*"]
rotate[p4_, p2_] := Evaluate[Simplify@RotationTransform[1. Pi/3, p2][p4]];
generate[p1_, p5_] := Module[{p2, p3, p4},
p2 = (p5 - p1)/3 + p1;
p4 = 2 (p5 - p1)/3 + p1;
p3 = rotate[p4, p2];
{p1, p2, p3, p4}];
上述代码中,一定要用浮点数计算,因为这样才会比较高效率的得到我们需要的数据。当然了,上述代码即使用了浮点数计算,也是比较慢的(其实在本文中,上述代码的运行速度足够了,因为我们最终目的是画图,所以并不需要迭代很多次,画到5/6阶就足够了)。仔细观察上述代码,可以发现上述代码其实就是大量的加减乘除,所以可以考虑用编译来加速。顺便打个广告(求广告费~),对于编译已经有一定的了解但是还不够深入的人,可以看一下这个帖子,相信能有一定的帮助。上述代码的编译版本如下:
Clear["Global`*"]
rotate = Compile[{{p4, _Real, 1}, {p2, _Real, 1}},
{{ 0.5, -0.8660254037844386}.p4 + {0.5, 0.8660254037844386}.p2,
{0.8660254037844386, 0.5}.p4 + {-0.8660254037844386, 0.5}.p2}];
generate = Compile[{{p1, _Real, 1}, {p5, _Real, 1}},
Module[{p2, p3, p4},
p2 = (p5 - p1)/3 + p1;
p4 = 2 (p5 - p1)/3 + p1;
p3 = rotate[p4, p2];
{p1, p2, p3, p4}]
];
初始条件下就是一条线段啦,所以data[0]=N@{ {0, 0}, {1, 0}},注意,加个N让后面的计算都是浮点数计算。然后就是迭代啦。
data[0]=N@{{ 0, 0}, {1, 0}};
data[n_] := data[n] = Flatten[{generate @@@ Partition[data[n - 1], 2, 1], {{{ 1, 0}}}}, 2];
Partition就是把一系列点分成2个1组,然后generate上去,当然,别忘了由于我们只保存了p1,p2,p3,p4,所以{1,0}这个点就只能Flatten进去啦。现在,我们就可以画图了,例如这样Graphics[Line@data[3]]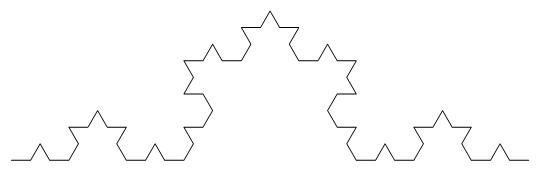
到现在,静态的图我们就已经画出来了。接下来就是考虑如何动态化的过程啦。这个动态化,说难也不难,说简单也不简单。对于学过物理的,应该都知道,如果已知状态A和状态B,0时刻处于状态A,1时刻处于状态B,0到1时刻是均匀变化的,那么任意时刻,状态就是(1-t)A+tB啦。比如玻色子费米子任意子的自旋、匀速运动等等。在这里的动态化,不就是一个点的匀速运动嘛!所以我们就写一个代码啦,如果已知1时刻的5个点,那么0时刻不就是p3点和p2或p4重合嘛,0到1时刻的中间任意时刻,就是这么一个状态,
move[{p1_, p2_, p3_, p4_, p5_}, t_] := {{p1, p2, (1 - t) p4 + t p3}, {(1 - t) p2 + t p3, p4, p5}};
举个简单的例子示意一下
Manipulate[Graphics[Line@move[{{ 0, 0}, {1/3, 0}, {0.5, 0.289}, {2/3, 0}, {1, 0}}, t],
PlotRange -> {{ 0, 1}, {-0.1, 0.3}}], {t, 0, 1}]
move函数是接收5个点,实际上数据集里包含很多点啊,所以又轮到Partition上场了。
AllMove[data_, t_] := move[#, t] & /@ Partition[data, 5, 4];
再举个简单的例子示意一下
Manipulate[Graphics@Line@Flatten[AllMove[data[2], t], 1], {t, 0, 1}]
在上面,data[2]里面的2是固定的,但是实际上这个2应该是从1取到5的正整数,AllMove里的第二个参数,也应该是从0变化到1,再变成0,再变化到1的。所以,我们就用到了Quotient和Mod。
newdata[t_] := Flatten[AllMove[data[Quotient[t + 1, 1]], Mod[t, 1]], 1];
最后,画图并且美化一下就OK啦。
Manipulate[ListLinePlot[newdata[t], PlotRange -> {{ 0, 1}, {-0.02, 0.3}}, AspectRatio -> 0.32,
Axes -> False, PlotStyle -> RGBColor[0.353, 0.741, 0.913], ImageSize -> {500, 200}],
{t, 0, 4, 0.03}, SaveDefinitions -> True]
想输出GIF动态图片的话,运行下面代码就搞定啦。注意这是在当前笔记本路径下保存GIF的,所以如果你是新建nb的话,下面这个代码会报错的,可以先保存nb再运行,或者修改一下Export的路径。
alldata = Table[newdata[t], {t, 0, 4, 0.02}];
pic = ListLinePlot[#, PlotRange -> { {0, 1}, {-0.02, 0.3}}, AspectRatio -> 0.32, Axes -> False,
PlotStyle -> RGBColor[0.353, 0.741, 0.913], ImageSize -> {500, 200}] & /@ alldata;
Export[NotebookDirectory[] <> "Koch.gif", pic, "DisplayDurations" -> 1/60]
最终的全部代码为:
Clear["Global`*"]
rotate[p4_, p2_] := Evaluate[Simplify@RotationTransform[1. Pi/3, p2][p4]];
generate[p1_, p5_] := Module[{p2, p3, p4},
p2 = (p5 - p1)/3 + p1;
p4 = 2 (p5 - p1)/3 + p1;
p3 = rotate[p4, p2];
{p1, p2, p3, p4}];
data[0]=N@{{ 0, 0}, {1, 0}};
data[n_] := data[n] = Flatten[{generate @@@ Partition[data[n - 1], 2, 1], {{{ 1, 0}}}}, 2];
move[{p1_, p2_, p3_, p4_, p5_}, t_] := {{p1, p2, (1 - t) p4 + t p3}, {(1 - t) p2 + t p3, p4, p5}};
AllMove[data_, t_] := move[#, t] & /@ Partition[data, 5, 4];
newdata[t_] := Flatten[AllMove[data[Quotient[t + 1, 1]], Mod[t, 1]], 1];
Manipulate[ListLinePlot[newdata[t], PlotRange -> {{ 0, 1}, {-0.02, 0.3}}, AspectRatio -> 0.32,
Axes -> False, PlotStyle -> RGBColor[0.353, 0.741, 0.913], ImageSize -> {500, 200}],
{t, 0, 4, 0.03},SaveDefinitions -> True]
alldata = Table[newdata[t], {t, 0, 4, 0.02}];
pic = ListLinePlot[#, PlotRange -> { {0, 1}, {-0.02, 0.3}}, AspectRatio -> 0.32, Axes -> False,
PlotStyle -> RGBColor[0.353, 0.741, 0.913], ImageSize -> {500, 200}] & /@ alldata;
Export[NotebookDirectory[] <> "Koch.gif", pic, "DisplayDurations" -> 1/60]

